机器学习之线性回归算法

机器学习中的线性回归方程算法是一种基础的预测性建模技术，它研究的是因变量（目标变量）与自变量（特征变量）之间的关系。线性回归试图找到一条最佳的直线（在多维空间中可能是超平面），这条直线能够尽可能地拟合数据点，从而能够预测新的数据点的目标值。

一、线性回归模型的基本原理

线性回归是一种统计学和机器学习中常用的方法，其核心在于通过建立自变量（独立变量）和因变量（响应变量）之间的线性关系来预测或解释因变量的变化。这种模型假设因变量是自变量的线性组合，再加上一个误差项。线性回归模型的数学表达式通常写为：

Y = β0 + β1X1 + β2X2 + ... + βnXn + ε

其中，Y是因变量，X1, X2, ..., Xn是自变量，β0, β1, ..., βn是模型的参数（或系数），这些参数决定了自变量对因变量的影响，而ε是误差项，表示无法通过自变量解释的Y的部分。

线性回归的目标是找到最佳拟合线，即能够最小化实际数据点与预测值之间误差的直线。这通常通过最小二乘法来实现，从而得到最优的回归系数。

而如果有多个变量，也就是n元线性回归的形式如下：

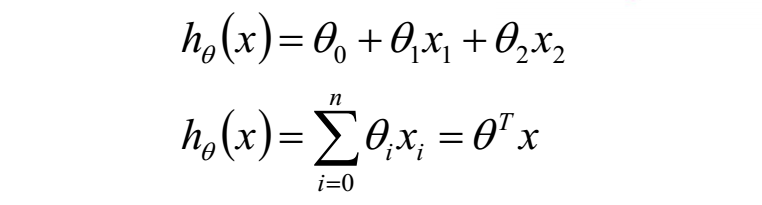
n元线性回归

在这里b被截断然后用θ0代替，同时数据集X也需要添加一列1用于与θ0相乘，表示+b。最后写成矩阵的形式就是θ的转置乘以x。其中如果数据集有n个特征，则θ就是n+1维的向量并非矩阵，其中包括截断b。

二、线性回归的目的

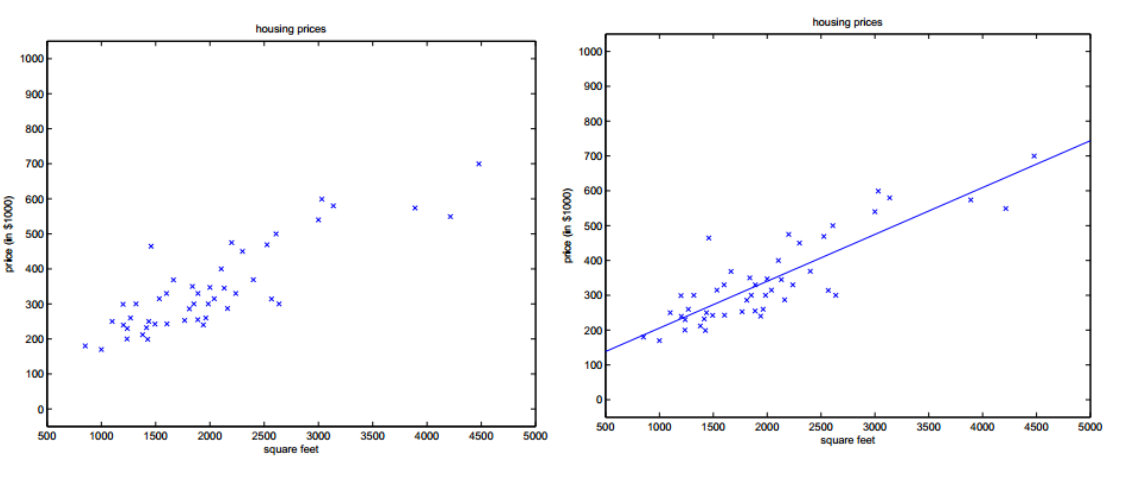
线性回归的目的就是求解出合适的θ，在一元的情况下拟合出一条直线（多元情况下是平面或者曲面），可以近似的代表各个数据样本的标签值。所以最好的直线要距离各个样本点都很接近，而如何求出这条直线就是我们需要解决的重点

三、线性回归模型的计算

在把一组数据x和y带入模型中，显然最好的效果应该是模型拟合出的那条直线尽可能穿过更多的点才是，需要对模型进行优化，这里要引入一个概念。

损失函数：是用来估量你模型的预测值 f(x)与真实值 YY 的不一致程度，损失函数越小，模型的效果就越好。它的具体形式如下：

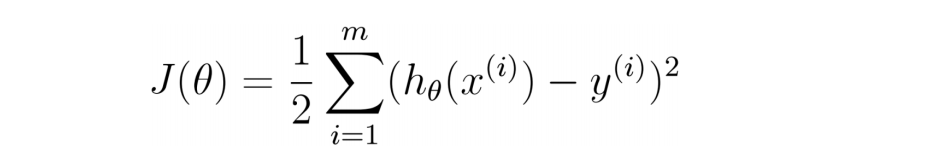
其中hθ(x^(i))代表每个样本通过我们模型的预测值，y^(i)代表每个样本标签的真实值，m为样本个数。因为模型预测值和真实值间存在误差e，可以写作：

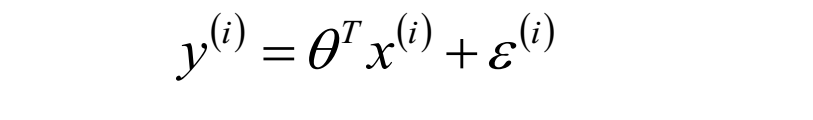
(预测值-真实值)的平法和的平均值，换句话说就是点到直线距离和最小。

四、梯度下降法

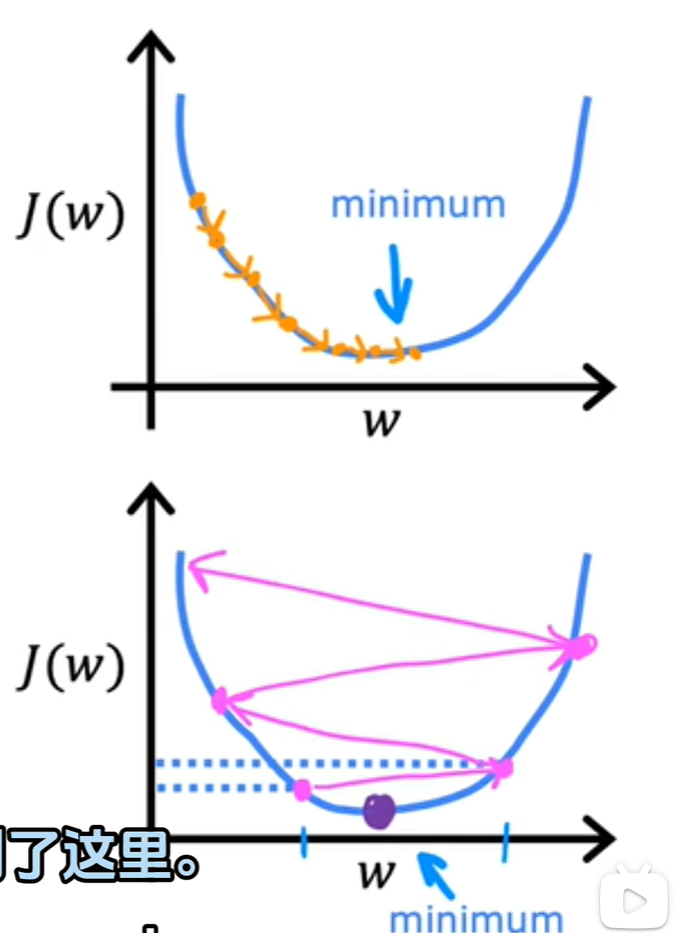
梯度下降法的基本思想可以类比为一个下山的过程，如下图所示函数看似为一片山林，红色的是山林的高点，蓝色的为山林的低点，蓝色的颜色越深，地理位置越低，则图中有一个低点，一个最低点。

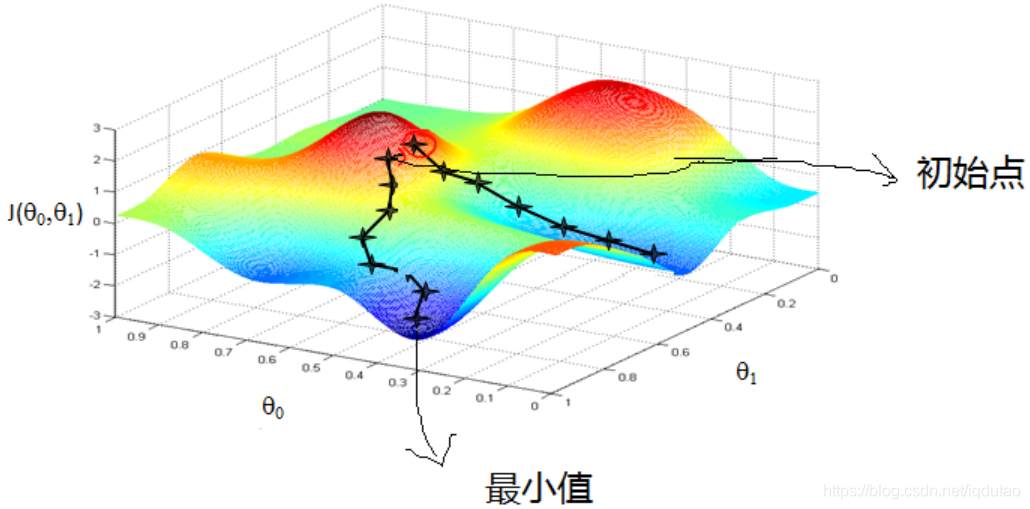
定义一个公式如下图所示，J是关于Θ的一个函数，我们在山林里当前所处的位置为Θ0点，要从这个点走到J的最小值点，也就是山底。首先我们先确定前进的方向，也就是梯度的反向，然后走一段距离的步长，也就是α，走完这个段步长，就到达了Θ1这个点。

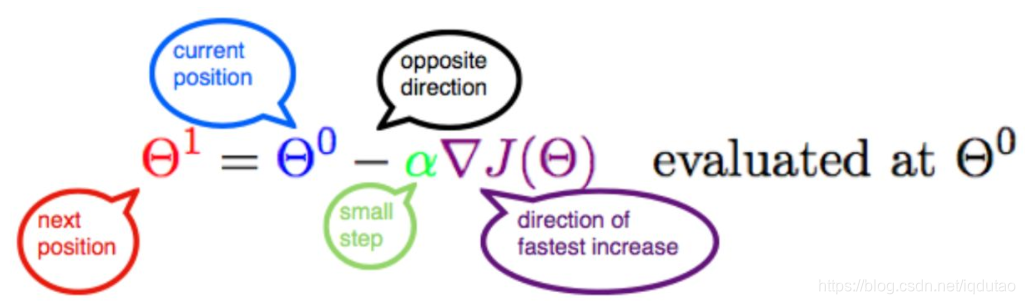
α在梯度下降算法中被称作为学习率或者步长，意味着我们可以通过α来控制每一步走的距离，以保证不要步子跨的太大，其实就是不要走太快，错过了最低点。同时也要保证不要走的太慢，导致太阳下山了，还没有走到山下。所以α的选择在梯度下降法中往往是很重要的！α不能太大也不能太小，太小的话，可能导致迟迟走不到最低点，太大的话，会导致错过最低点