损失函数（Loss Function）简介(1)

损失函数介绍

解决一个机器学习问题主要有两个部分：数据和算法。

算法又由三个部分组成：假设函数、损失函数和算法优化。

损失函数（Loss Function）：用于计算损失的函数。在机器学习中，通常把模型关于单个样本预测值与真实值的差称为损失，损失越小，模型越好。故损失函数就是用来衡量模型预测值与真实标签之间差异的函数。不同的任务和模型可能需要不同的损失函数。

常见的损失函数

1.对数损失函数（Logloss）

对数损失函数（Logloss，也叫二元交叉熵损失，LR），是机器学习中常用的一种损失函数之一，主要适用于二分类、逻辑回归问题。它用于衡量模型预测结果与实际标签之间的差异。

对数损失基于信息论中的交叉熵概念，用于度量两个概率分布之间的相似性。在二分类问题中，通常使用0和1表示实际标签，而模型的预测结果是一个介于0和1之间的概率值。对数损失通过计算实际标签和模型预测结果的交叉熵来评估模型的性能。

对数函数可以表示为：

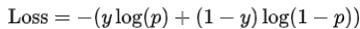
其函数标准形式为：

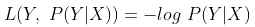
下面是其Python应用示例：

import numpy as np
import matplotlib.pyplot as plt
 
def log_loss(y_true, p_pred):
    epsilon = 1e-10  # 添加一个小的常数以避免log(0)计算错误
    return - (y_true * np.log(p_pred + epsilon) + (1 - y_true) * np.log(1 - p_pred + epsilon))
 
# 模拟数据
num_samples = 1000
 
np.random.seed(42)
y_true = np.random.randint(2, size=num_samples)  # 随机生成0和1的实际标签
p_pred = np.random.rand(num_samples)  # 模型预测的概率
 
loss = log_loss(y_true, p_pred)
 
# 计算平均损失
average_loss = np.mean(loss)
 
# 绘制损失函数图形
plt.plot(range(num_samples), loss, 'bo', markersize=2)
plt.xlabel('Sample')
plt.ylabel('Log Loss')
plt.title('Log Loss for each Sample')
plt.axhline(average_loss, color='r', linestyle='--', label='Average Loss')
plt.legend()
plt.show()
 
print(f'Average Loss: {average_loss}')

2. cross-entropy loss 交叉熵损失函数

交叉熵损失是机器学习中常用的一种损失函数，主要应用于ID3（决策树）和分类问题。它用于衡量模型预测结果与实际标签之间的差异。

交叉熵损失基于信息论中的交叉熵概念，用于度量两个概率分布之间的相似性。在分类问题中，我们将实际标签表示为一个one-hot向量，即只有一个元素为1，其余元素为0；而模型的预测结果通常是一个概率分布。交叉熵损失通过计算实际标签和模型预测结果之间的交叉熵来评估模型的性能。交叉熵越小，实际值与预测值的概率的分布越接近。

结合给定的两个概率分布p和q，通过q来表示p的交叉熵为：

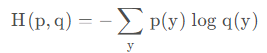
交叉熵刻画的是两个概率分布之间的距离，或可以说其刻画的是通过概率分布q来表达概率分布p的困难程度，p代表正确答案，q代表的是预测值，交叉熵越小，两个概率的分布越接近。

以下是一个多分类问题的例子，使用交叉熵损失进行模型训练：

import numpy as np
import matplotlib.pyplot as plt
 
def cross_entropy_loss(y_true, p_pred):
    epsilon = 1e-10  # 添加一个小的常数以避免log(0)计算错误
    return -np.sum(y_true * np.log(p_pred + epsilon), axis=1)
 
# 模拟数据
num_samples = 1000
num_classes = 5
 
np.random.seed(42)
y_true = np.eye(num_classes)[np.random.choice(num_classes, num_samples)]  # 生成随机的one-hot标签
p_pred = np.random.rand(num_samples, num_classes)  # 模型预测的概率
 
loss = cross_entropy_loss(y_true, p_pred)
 
# 计算平均损失
average_loss = np.mean(loss)
 
# 绘制损失函数图形
plt.plot(range(num_samples), loss, 'bo', markersize=2)
plt.xlabel('Sample')
plt.ylabel('Cross-Entropy Loss')
plt.title('Cross-Entropy Loss for each Sample')
plt.axhline(average_loss, color='r', linestyle='--', label='Average Loss')
plt.legend()
plt.show()
 
print(f'Average Loss: {average_loss}')

3. 置信度损失函数（confidence loss）

置信度损失函数（confidence loss）是YOLO算法中用来衡量预测框与真实框之间匹配程度的损失函数之一。它主要衡量的是预测框的置信度预测值与真实值之间的差异。置信度损失由两部分组成：一部分是预测框包含目标的置信度，另一部分是预测框不包含目标的置信度。

置信度损失的计算

置信度损失可以表示为：

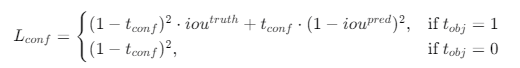
其中：

• t_conf​ 是预测框的置信度。

• iou^truth 是预测框与真实框之间的交并比（IOU），当预测框包含目标时，即检测到目标。

• iou^pred 是预测框与真实框之间的交并比（IOU），当预测框不包含目标时，即未检测到目标。

• t_obj​ 是一个指示变量，如果网格单元包含目标，则为1；否则为0。

具体的问题示例

假设我们有一个目标检测任务，其中有一个真实框和一个预测框。真实框的坐标是(100, 100, 150, 150)，预测框的坐标是(120, 120, 140, 140)。预测框的置信度是0.8，真实框与预测框的IOU是0.5。

基于PyTorch深度学习，运用置信度损失函数进行模型训练

import torch
import torch.nn as nn
import torch.optim as optim

# 定义置信度损失函数
class ConfidenceLoss(nn.Module):
    def __init__(self):
        super(ConfidenceLoss, self).__init__()

    def forward(self, pred_conf, target_conf, pred_boxes, target_boxes, obj_present):
        # 计算IOU
        def box_iou(box1, box2):
            # 计算交集面积
            inter_x1 = torch.max(box1[0], box2[0])
            inter_y1 = torch.max(box1[1], box2[1])
            inter_x2 = torch.min(box1[2], box2[2])
            inter_y2 = torch.min(box1[3], box2[3])
            inter_area = torch.clamp(inter_x2 - inter_x1 + 1, min=0) * torch.clamp(inter_y2 - inter_y1 + 1, min=0)
            
            # 计算各自面积
            box1_area = (box1[2] - box1[0] + 1) * (box1[3] - box1[1] + 1)
            box2_area = (box2[2] - box2[0] + 1) * (box2[3] - box2[1] + 1)
            
            # 计算IOU
            iou = inter_area / (box1_area + box2_area - inter_area)
            return iou

        # 计算置信度损失
        conf_loss = 0
        for i in range(pred_conf.size(0)):
            if obj_present[i]:
                iou = box_iou(pred_boxes[i], target_boxes[i])
                conf_loss += (1 - target_conf[i]) * torch.pow(iou, 2) + pred_conf[i] * torch.pow(1 - iou, 2)
            else:
                conf_loss += torch.pow(1 - pred_conf[i], 2)

        return conf_loss / pred_conf.size(0)

# 假设数据
pred_conf = torch.tensor([0.8])  # 预测框的置信度
target_conf = torch.tensor([1.0])  # 真实框的置信度
pred_boxes = torch.tensor([[120, 120, 140, 140]])  # 预测框的坐标
target_boxes = torch.tensor([[100, 100, 150, 150]])  # 真实框的坐标
obj_present = torch.tensor([1])  # 指示变量，表示是否有目标

# 实例化损失函数和优化器
criterion = ConfidenceLoss()
optimizer = optim.SGD(params=[], lr=0.01)

# 计算损失
loss = criterion(pred_conf, target_conf, pred_boxes, target_boxes, obj_present)
print("Confidence Loss:", loss.item())

# 假设有一个简单的模型参数需要优化
params = torch.randn(1, requires_grad=True)
optimizer.param_groups[0]['params'].append(params)

# 反向传播和优化
loss.backward()
optimizer.step()